Training

Training loops for KGE models using multi-modal information.

Throughout the following explanations of training loops, we will assume the set of entities \(\mathcal{E}\), set of relations \(\mathcal{R}\), set of possible triples \(\mathcal{T} = \mathcal{E} \times \mathcal{R} \times \mathcal{E}\). We stratify \(\mathcal{T}\) into the disjoint union of positive triples \(\mathcal{T^{+}} \subseteq \mathcal{T}\) and negative triples \(\mathcal{T^{-}} \subseteq \mathcal{T}\) such that \(\mathcal{T^{+}} \cap \mathcal{T^{-}} = \emptyset\) and \(\mathcal{T^{+}} \cup \mathcal{T^{-}} = \mathcal{T}\).

A knowledge graph \(\mathcal{K}\) constructed under the open world assumption contains a subset of all possible positive triples such that \(\mathcal{K} \subseteq \mathcal{T^{+}}\).

Assumptions

Open World Assumption

When training under the open world assumption (OWA), all triples that are not part of the knowledge graph are considered unknown (e.g., neither positive nor negative). This leads to under-fitting (i.e., over-generalization) and is therefore usually a poor choice for training knowledge graph embedding models [nickel2016review]. PyKEEN does not implement a training loop with the OWA.

Warning

Many publications and software packages use OWA to incorrectly refer to the stochastic local closed world assumption (sLCWA). See below for an explanation.

Closed World Assumption

When training under the close world assumption (CWA), all triples that are not part of the knowledge graph are considered as negative. As most knowledge graphs are inherently incomplete, this leads to over-fitting and is therefore usually a poor choice for training knowledge graph embedding models. PyKEEN does not implement a training loop with the CWA.

Local Closed World Assumption

When training under the local closed world assumption (LCWA; introduced in [dong2014]), a particular subset of triples that are not part of the knowledge graph are considered as negative.

Strategy	Local Generator	Global Generator
Head	\(\mathcal{T}_h^-(r,t)=\{(h,r,t) \mid h \in \mathcal{E} \land (h,r,t) \notin \mathcal{K} \}\)	\(\bigcup\limits_{(\_,r,t) \in \mathcal{K}} \mathcal{T}_h^-(r,t)\)
Relation	\(\mathcal{T}_r^-(h,t)=\{(h,r,t) \mid r \in \mathcal{R} \land (h,r,t) \notin \mathcal{K} \}\)	\(\bigcup\limits_{(h,\_,t) \in \mathcal{K}} \mathcal{T}_r^-(h,t)\)
Tail	\(\mathcal{T}_t^-(h,r)=\{(h,r,t) \mid t \in \mathcal{E} \land (h,r,t) \notin \mathcal{K} \}\)	\(\bigcup\limits_{(h,r,\_) \in \mathcal{K}} \mathcal{T}_t^-(h,r)\)

Most articles refer exclusively to the tail generation strategy when discussing LCWA. However, the relation generation strategy is a popular choice in visual relation detection domain (see [zhang2017] and [sharifzadeh2019vrd]). However, PyKEEN additionally implements head generation since PR #602.

Stochastic Local Closed World Assumption

When training under the stochastic local closed world assumption (SLCWA), a random subset of the union of the head and tail generation strategies from LCWA are considered as negative triples. There are a few benefits from doing this:

Reduce computational workload
Spare updates (i.e., only a few rows of the embedding are affected)
Ability to integrate new negative sampling strategies

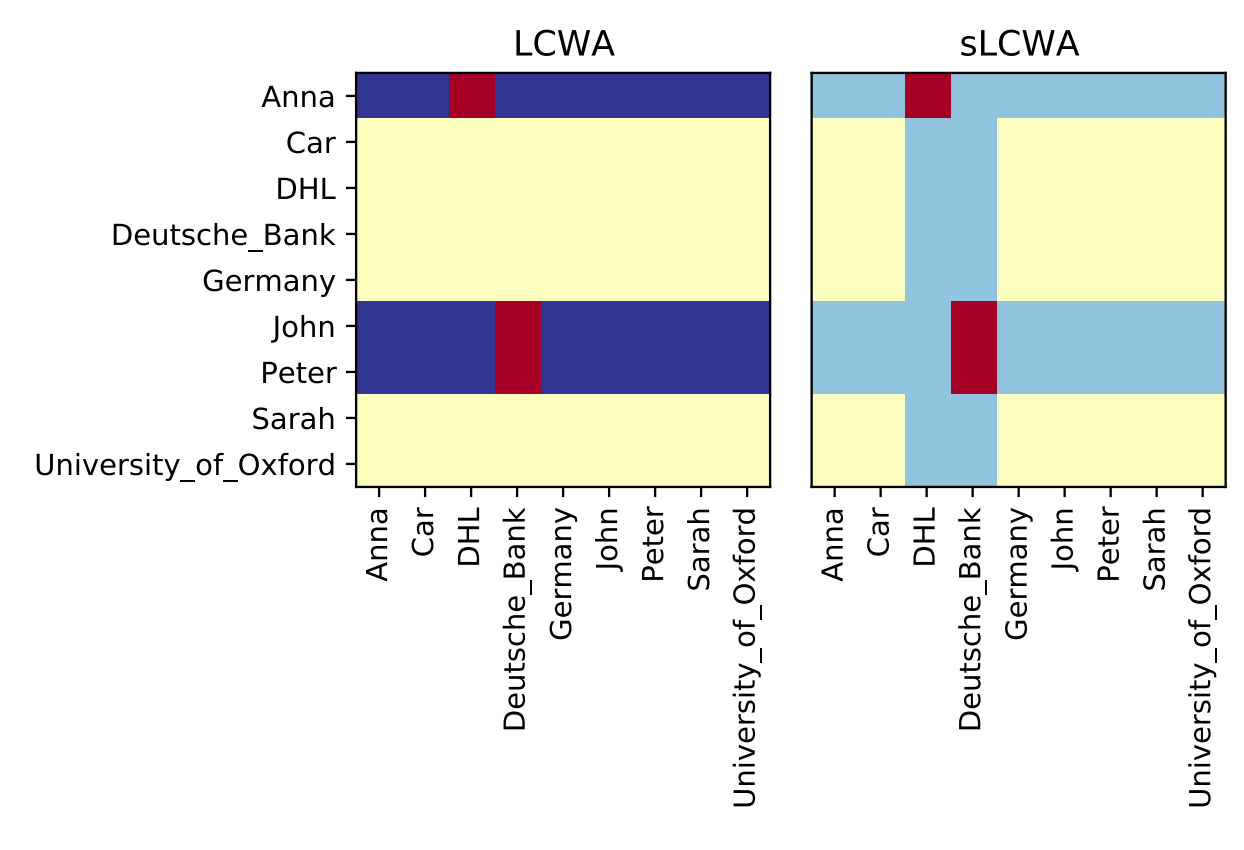
There are two other major considerations when randomly sampling negative triples: the random sampling strategy and the filtering of positive triples. A full guide on negative sampling with the SLCWA can be found in pykeen.sampling. The following chart from [ali2020a] demonstrates the different potential triples considered in LCWA vs. sLCWA based on the given true triples (in red):

Batch-Local Closed World Assumption

When training under the batch-local closed world assumption (BCWA), all combinations of heads, relations, and tails occurring in a batch of training triples are scored, and those which are not training triples are considered as negative. See BatchCWATrainingLoop for details.

For example, consider a knowledge graph with the training triples (Alice, knows, Bob), (Bob, likes, Carol), (Alice, likes, Carol), and (Carol, knows, Dave), and a batch with the first two triples. The batch contains the heads {Alice, Bob}, the relations {knows, likes}, and the tails {Bob, Carol}, and BCWA scores all \(2 \cdot 2 \cdot 2 = 8\) combinations of them. Three of them are training triples and thus positive: the two batch triples, and (Alice, likes, Carol), which is not part of the batch. The remaining five are negative. For tail prediction, each (head, relation)-pair is one row, and the batch’s tails are the candidates:

(head, relation)	Bob	Carol
(Alice, knows)	1	0
(Alice, likes)	0	1
(Bob, knows)	0	0
(Bob, likes)	0	1

In comparison, the CWA would score all \(4 \cdot 2 \cdot 4 = 32\) possible triples, and the LCWA would score each (head, relation)-pair of the batch with all four entities as tails. Under the BCWA, Dave is never scored, since he does not occur in the batch. Hence, it only requires the representations of the batch’s entities and relations, which are needed to score the batch triples anyway.

Classes

`BatchCWATrainingLoop`(*[, target])	A training loop that is based upon the batch-local closed world assumption (BCWA).
`LCWATrainingLoop`(*[, target])	A training loop that is based upon the local closed world assumption (LCWA).
`NonFiniteLossError`	An exception raised for non-finite loss values.
`OptimizerClearedError`	An exception raised when the optimizer is required, but has been cleared.
`OptimizerNotRecreatableError`	An exception raised when a pre-instantiated optimizer or LR scheduler would need to be re-created.
`SLCWATrainingLoop`(*[, negative_sampler, ...])	A training loop that uses the stochastic local closed world assumption training approach.
`SymmetricLCWATrainingLoop`(model, triples_factory)	A "symmetric" LCWA scoring heads and tails at once.
`TrainingLoop`(model, triples_factory[, ...])	A training loop.

Variables

training_loop_resolver

A resolver for training loops

Class Inheritance Diagram

Callbacks

Training callbacks.

Training callbacks allow for arbitrary extension of the functionality of the TrainingLoop without subclassing it. Each callback instance has a loop attribute that allows access to the parent training loop and all of its attributes, including the model. The interaction points are similar to those of Keras.

Examples

The following are vignettes showing how PyKEEN’s training loop can be arbitrarily extended using callbacks. If you find that none of the hooks in the TrainingCallback help do what you want, feel free to open an issue.

Reporting Batch Loss

It was suggested in Issue #333 that it might be useful to log all batch losses. This could be accomplished with the following:

from pykeen.training import TrainingCallback

class BatchLossReportCallback(TrainingCallback):
    def on_batch(self, epoch: int, batch, batch_loss: float):
        print(epoch, batch_loss)

Implementing Gradient Clipping

Gradient clipping is one technique used to avoid the exploding gradient problem. Despite it being a very simple, it has several theoretical implications.

In order to reproduce the reference experiments on R-GCN performed by [schlichtkrull2018], gradient clipping must be used before each step of the optimizer. The following example shows how to implement a gradient clipping callback:

from pykeen.training import TrainingCallback
from pykeen.nn.utils import clip_grad_value_

class GradientClippingCallback(TrainingCallback):
    def __init__(self, clip_value: float = 1.0):
        super().__init__()
        self.clip_value = clip_value

    def pre_step(self, **kwargs: Any):
        clip_grad_value_(self.model.parameters(), clip_value=self.clip_value)

Classes

`CheckpointTrainingCallback`([schedule, ...])	Save checkpoints at user-specific epochs.
`EvaluationLoopTrainingCallback`(factory[, ...])	A callback for regular evaluation using new-style evaluation loops.
`EvaluationTrainingCallback`(*, evaluation_triples)	A callback for regular evaluation.
`GradientAbsClippingTrainingCallback`(clip_value)	A callback for gradient clipping before stepping the optimizer with `torch.nn.utils.clip_grad_value_()`.
`GradientNormClippingTrainingCallback`(max_norm)	A callback for gradient clipping before stepping the optimizer with `torch.nn.utils.clip_grad_norm_()`.
`MultiTrainingCallback`([callbacks, ...])	A wrapper for calling multiple training callbacks together.
`StopperTrainingCallback`(stopper, *, ...[, ...])	An adapter for the `Stopper`.
`TrackerTrainingCallback`()	An adapter for the `ResultTracker`.
`TrainingCallback`()	An interface for training callbacks.

Variables

`TrainingCallbackHint`	A hint for constructing a `MultiTrainingCallback`
`callback_resolver`	A resolver for training callbacks

Class Inheritance Diagram

Learning Rate Schedulers

Learning Rate Schedulers available in PyKEEN.

Classes

LRScheduler(optimizer[, last_epoch])

Base class for all learning rate schedulers.

Variables

`lr_scheduler_resolver`	Resolve from a list of classes.
`lr_schedulers_hpo_defaults`	The default strategy for optimizing the lr_schedulers' hyper-parameters, based on `torch.optim.lr_scheduler.LRScheduler`